Формирование панорамного изображения с учетом параллакса при известной модели окружающего мира
Аннотация
Дата поступления статьи: 25.09.2013Приведен краткий обзор существующих систем формирования панорамных изображений, и показано их ограничение применительно к задаче формирования панорамного изображения от разнесенных в пространстве камер в режиме реального времени. Представлен алгоритм формирования панорамного изображения, позволяющей учитывать влияние параллакса и основанный на разработанной математической модели видеосистемы кругового обзора. Модель учитывает взаимное расположение камер, их внутренние параметры и характерные геометрические искажения, а также позволяет учесть модель окружающего мира.
Ключевые слова: панорамное изображение, видеосистема кругового обзора, модель камеры, геометрические искажения камеры, параллакс
05.13.18 - Математическое моделирование, численные методы и комплексы программ
Видеосистемой кругового обзора будем называть систему, отображающую окружающую обстановку с углом обзора до 360° по горизонтали в реальном времени и для всех направлений одновременно. Подобные системы могут устанавливаться на мобильные платформы (автомобили, роботизированные тележки) для облегчения задач вождения [1] или осуществления удаленного управления транспортным средством. Изображение с большим углом обзора, называемое панорамой, позволяет ценой уменьшения детализации и внесения определенных геометрических искажений представить на плоскости окружающее наблюдателя пространство. Изображения с большим углом обзора можно получить с помощью различных оптических устройств (рис. 1): широкоугольных объективов типа «рыбий глаз» [2], у которых угол обзора составляет около 180° вдоль диагонали кадра; панорамных катадиоптрических систем, в основе которых лежит зеркало сферической или другой формы [3], позволяющее получить изображение с углами обзора до 360° по горизонтали и более 100° по вертикали. Основной недостаток подобных оптических устройств: невысокое и неравномерное разрешение итоговой панорамы. По этим причинам широкое распространение получили методы формирования панорамы из нескольких перекрывающихся изображений, полученных камерой, вращающейся вокруг оптического центра объектива [4]. Выполнение этого требования означает, что исходные изображения лишены параллакса; в этом случае на формируемой панораме идеально совместятся как близко, так и далеко расположенные объекты. С целью минимизации параллакса в видеосистемах кругового обзора, где невозможно все камеры разместить в одной точке, камеры стараются расположить как можно компактнее [5] или используют систему зеркал, вокруг которой располагаются камеры [6].
Подобное беспараллаксное размещение камер вынуждает размещать видеосистему кругового обзора сверху, где обзор не закрывается элементами конструкции, что в определенных случаях вступает в конфликт с конструкторскими или дизайнерскими решениями по установке камер, а также повышает заметность системы. В этих случаях камеры приходится располагать далеко друг от друга (например, по бортам транспортного средства, где их обзор не ограничивают элементы конструкции), следовательно, влиянием параллакса нельзя пренебречь.
 |
|
|
|
|
а) |
б) |
в) |
г) |
|
Рис. 1. Разнообразие конструкций, используемых для формирования панорам: а) объектив типа «рыбий глаз»; б) параболическое зеркало; в) компактное размещение камер; г) система зеркал. |
|||
Для получения панорамного изображения с учетом параллакса необходимо иметь информацию о внутренних и внешних параметрах камеры, которые могут быть оценены в результате калибровки камер и всей системы, а также информацию об удаленности объектов сцены. На основе этой информации будет производиться преобразование входных изображений.
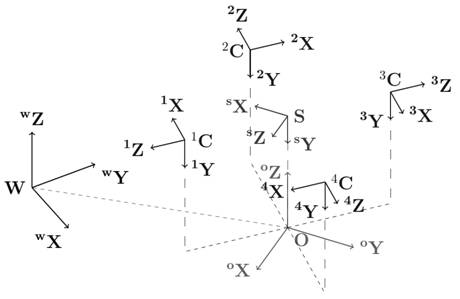
Введем следующие трехмерные системы координат (рис. 2). В глобальной системе координат W (приведена для общности, в дальнейшем эта система координат применяться не будет) перемещается мобильная платформа, к которой привязана объектная система координат O. На платформе в системе координат O расположено размещены камеры с соответствующими камероцентрическими системами координат kC, где k – номер камеры. Наконец, относительно O определена наблюдательная система координат S, относительно которой производится построение панорамы. Все трехмерные системы координат являются правыми. Оси OX, OY, OZ соответственно направлены вправо, вперед и вверх относительно мобильной платформы; оси kX, kY, kZ, а также оси SX, SY, SZ соответственно направлены вправо и вниз от камеры (точки наблюдения), т.е. более далекие объекты имеют большие значения координаты Z. Кроме трехмерных систем координат будем использовать следующие двумерные системы координат: системы координат входных изображения kI, и система координат панорамного изображения P, которые образованы двумя перпендикулярными осями U и V, при этом ось U направлена вправо, а ось V направлена вниз.
Для получения панорамного изображения P из исходных изображений kI необходимо выполнить соответствующие геометрические преобразования, связывающие координаты точки на панораме Pu с координатами точки на входном изображении ku. Как правило, такую зависимость выражают в виде функции обратного отображения [7, с. 278], связывающего точки Pu и ku:
ku = kM−1(Pu).(1) |
|
|
|
|
|
Рис. 2. Используемые системы координат: глобальная система координат W; объектная система координат O; четыре камероцентрических системы координат 1C, 2C, 3C и 4C; наблюдательная система координат S. |
|
Функция обратного отображения (1) может быть представлена в виде последовательности преобразований:
1. Преобразование координат панорамного изображения Pu = (Pu, Pv) в координаты Sx = (Sx, Sy, Sz) наблюдательной системы координат S. Для этого удобно воспользоваться сферической системой координат с центром в точке S в которой точка Sx, описывается углами азимута λ ∈ (−π; π] (угол между осью SZ и проекцией вектора Sx на плоскость SXSZ) и высоты φ ∈ (−π/2; π/2) (угол, образованный вектором Sx и его проекцией на плоскость SXSZ) и расстоянием ρ (длина вектора Sx). Углы λ и φ зависят от координат (Pu, Pv) и определяются проекцией панорамного изображения. Например, для сферической (более корректный термин цилиндрической равнопромежуточной) проекции углы λ и φ пропорциональны координатам (Pu, Pv) [8]:
λ = (Pu −u0) / f,(2) φ = (Pv −u0) / f, |
|
где f – масштабирующий множитель, (u0, v0) – координаты точки на панорамном изображении, для которой угловые координаты λ и φ равны 0. Для панорамного изображения с углом охвата 360° по вертикали масштабирующий множитель целесообразно брать таким, чтобы ширина панорамы w = 2 π fбыла целым числом. В этом случае при замыкании панорамы в кольцо ее края совпадут. Третья координата – расстояние ρ – может быть задана априорно или оценена различными методами, и предполагается известной и зависящей от угловых координат:
ρ = f(λ, φ).(3) |
|
Переход от сферических координат (λ, φ, ρ) к координатам (Sx, Sy, Sz) осуществляется по известным формулам перехода от сферической системы координат к декартовой:
Sx = ρ cos φ sin λ, Sy = ρ sin φ, (4) Sz = ρ cos φ cos λ. |
|
2. Переход от наблюдательной системы координат S к объектной системе координат O осуществляется с помощью выражения вида
Ox = [SR | St] Sx,(5) |
|
где SR и St – матрица поворота и вектор переноса, определяющие переход от наблюдательной системы координат к объектной. Положение точки наблюдения может быть выбрано произвольно.
3. Переход к системе координат камеры kC из объектной системы координат O осуществляется аналогично (4). Для этого должны быть известны внешние параметры камер kR и kt, которые могут быть найдены в процессе калибровки видеосистемы кругового обзора:
kx = [kR | kt] Sx.(6) |
|
4. Проективное преобразование, осуществляющее переход от трехмерных координат kx = (kx, ky, kz) к двумерным нормированным координатам ku' = (ku', kv'), где
ku' = kx / kz,(7) kv' = ky / kz. |
|
5. Исправление геометрических искажений (дисторсии) камеры необходимо для компенсации искажений, вносимых широкоугольной оптикой. Модель искажений выбирается в зависимости от характеристик объектива. Например, может применяться следующая модель исправления дисторсии, определяемая тремя коэффициентами радиальных искажений k1, k2, k3 и двумя коэффициентами тангенциальных искажений p1 и p2 [9, с. 396] (для краткости верхние индексы k опущены):
u'' = u' (1 + k1 r2 + k2 r4 + k3 r6) + 2 p1 u' v' + p2 (r2 + 2u'2), v'' = v'(1 + k1 r2 + k2 r4 + k3 r6) + 2 p2 u' v' + p1 (r2 + 2v'2),(8) r2 = u'2 + v'2. |
|
здесь ku'' = (ku'', kv'') – координаты точки с коррекцией геометрических искажений.
6. Переход к координатам изображения ku = (ku, kv) осуществим при известных внутренних параметрах каждой камеры:
ku = kfu ku'' + kcu,(9) kv = kfv kv'' + kcv, |
|
где kfu, kfv – фокальные расстояния по обеим осям (в общем случае, масштаб изображения по вертикали и горизонтали может отличаться); kcu, kcv – координаты точки пересечения оптической оси камеры и плоскости изображения.
Таким образом, функция обратного отображения (1), позволяющая перейти от координат на панораме к координатам изображения выбранной камеры, может быть представлена в виде последовательности операций (2)–(9) и параметризируется несколькими наборами параметров:
– внутренние параметры камеры (kfu, kfv, kcu, kcv) и
– коэффициенты дисторсии (kk1, kk2, kk3, kp1 и kp2) определяются в процессе индивидуальной калибровки каждой камеры системы обзора;
– внешние параметры камеры (матрица поворота kR и вектор переноса kt), которые могут быть получены при калибровки системы обзора [10];
– параметры системы координат, в которой строится панорама (SR и St), задающиеся произвольно;
– функцией расстояния до объектов сцены ρ = f(λ, φ), которую для меняющейся сцены необходимо оценивать динамически или же задавать априорно.
Для построения панорамного изображения необходимо иметь набор функций отображения kM−1(Pu) для каждого входного изображения. Значения этих функций целесообразно вычислить один раз и запомнить в соответствующих таблицах (при статической модели мира). Такой подход позволит формировать панорамное видеоизображение в реальном времени. Расчет значений функции kM−1(Pu) при формировании таблицы разумно предварить определением границ изображения на панораме, т.е. найти область определения функции kM−1(Pu). Возможный подход – последовательность операций, обратная (2)–(9) – осложнен тем, что функция расстояний до объектов сцены (3), а также моделирование дисторсии объектива (8) не имеют обратных преобразований, следовательно, необходим итеративный подход. Другой подход нахождения области определения функций: рассчитать их значения для уменьшенной панорамы, пересчитать их для полноразмерной панорамы и при необходимости уточнить.
Отдельного упоминания заслуживает модель окружающего мира. К сожалению, формирование картины окружающего мира в режиме реального времени весьма сложная задача, поэтому в данной статье ограничимся использованием заранее определенной статической модели окружающего мира. В качестве такой модели рассмотрим использование сферы заданного радиуса и «полусферы»: сферы, ограниченной снизу плоскостью (не обязательно проходящей через центр сферы).
На рис. 3 приведены примеры панорамного изображения, полученного в реальных условиях, для разных дальностей «сшивки». Можно заметить, что на близких расстояниях плохо совмещаются объекты на удалении, и наоборот.
 |
|
|
|
Рис. 3. – Панорамное изображение при разных дальностях «сшивки»: 20 м (сверху), бесконечная дальность (снизу). |
На рис. 4 показана укрупненная часть панорамного изображения при сшивке для сферической поверхности, и для «полусферы», ограниченной дорожной поверхностью. Положительные качества второго варианта отображения заключаются в увеличенной ширине дороги, лучшем совмещении близкорасположенных автомобилей. Недостатки представлены в виде характерных искажений объектов в нижней полусфере, особенно заметные на границах перехода плоскости в сферу.
 |
|
|
|
Рис. 4. – Центральная часть панорамы при «сшивке» на бесконечном расстоянии для сферической поверхности (сверху) и для «полусферы» (снизу). |
Таким образом, представленная модель видеосистемы кругового обзора позволяет формировать панорамное изображение для известной модели мира. Заранее рассчитанные функции преобразования (1) позволяют производить сшивку видеопанорамы в режиме реального времени. В различных ситуациях могут оказаться подходящими различные модели окружающего мира, разработанный алгоритм позволяет их динамически менять.
Литература
1. Рыжкина, Е.С. Период самостоятельного практического вождения молодых водителей – как наиболее опасный. [Электронный ресурс] // «Инженерный вестник Дона», 2012, №4 (часть 1). – Режим доступа: http://ivdon.ru/magazine/archive/n4p1y2012/1211 (доступ свободный) – Загл. с экрана. – Яз. рус.
2. Wang X., Wu K., Y. Cheng. Research on Virtual 3D Station based on Images // Applied Mathematics & Information Sciences. – 2013. – Vol. 7, No. 1L. – P. 225–231.
3. Folded catadioptric panoramic lens with an equidistance projection scheme / Gyeong-Il Kweon, Kwang Taek Kim, Geon-Hee Kim et al. // Applied Optics. – 2005. – Vol. 44. – P. 2759–2767.
4. Szeliski Richard. Image alignment and stitching: a tutorial // Found. Trends. Comput. Graph. Vis. – 2006. – Vol. 2, no. 1. – P. 1–104.
5. Utsugi K., Moriya T. A Camera Revolver for Improved Image Stitching // IARP Workshop on Machine Vision Applications. – 2002. – P. 261–264.
6. Geometrical Design Concept for Panoramic 3D Video Acquisition / O. Schreer, P. Kauff, P. Eisert et al. // 20th European Signal Processing Conference. – 2012. – P. 2757–2761.
7. Яне Б. Цифровая обработка изображений. – М. : Техносфера, 2007. – 584 с.
8. Weisstein, E. Cylindrical Equidistant Projection: [Электронный документ]. – (http://mathworld.wolfram.com/CylindricalEquidistantProjection.html). Проверено 15.06.2013
9. Bradski G., Kaehler A. Learning OpenCV.– Sebastopol: O’Reilly, 2008.– 555 p.
10. Толкачев, Д.С. Повышение точности калибровки внешних параметров видеокамеры [Электронный ресурс]. // «Инженерный вестник Дона», 2013, №3. – Режим доступа: http://ivdon.ru/magazine/archive/n3y2013/ (доступ свободный) – Загл. с экрана. – Яз. рус.